Class Notes on Gravitation (Physics 152)
Michael Fowler
I give here a summary of what I said in class—a more complete historical treatment of how these ideas developed (not essential for this course) can be found in my Galileo and Einstein lectures.
Galileo Analyzes a Cannonball Trajectory
Galileo was the first to understand the concept of acceleration in a precise way. He realized that a falling body picked up speed at a constant rate—in other words, it had constant acceleration. He called this “naturally accelerated motion”. He also made the crucial observation that, if air resistance and buoyancy can be neglected, all bodies fall with the same acceleration, bodies of different weights dropped together will reach the ground at the same time. This was a revolutionary idea—it was widely accepted up to his time that things fell at constant speed, and heavier things fell faster. (Why did they believe that? Because falling motion was too fast to observe easily, so they slowed it down by dropping things through water, for example, where buoyancy and resistance to movement are far more important. They didn’t appreciate how much that altered the nature of the motion.)
Galileo also realized that things fall at the same rate whether or not they have horizontal motion, if you drop a cannonball over a cliff it will fall 5 meters in the first second, if you fire it exactly horizontally at 100 meters per second, it will still fall 5 meters below a horizontal line in the first second. Meanwhile, its horizontal motion will be at a steady speed (again neglecting air resistance), it will go 100 meters in the first second, another 100 meters in the next second, and so on. Vertically, it falls 5 meters in the first second, 15 meters in the next second, then 25 and so on. Galileo drew a very nice graph of its position as a function of time, and proved the curve was parabolic. He worked out the range for given muzzle velocity and angle of firing. This was all of great interest to his employer, an Italian prince with military leanings.
Newton Puts the Cannon on a Very High Mountain
Newton asked the question:
what if we put the cannon on a really high (imaginary, of course!)
mountain above the atmosphere and fired the cannon really fast? It would still fall 5 meters in the first
second (ignoring the minor point that g goes down a bit on a really high
mountain), but if it’s going fast enough, don’t forget the curvature of
the earth! The surface of the earth curves
away below a horizontal line, so if we choose the right speed, after one second
the cannonball will have reached a point where the earth’s surface itself has
dropped away by 5 meters. In that case, the cannonball won’t have lost any
height at all! Furthermore, “vertically
down” has turned around a bit (it means perpendicular to the earth’s surface)
so the cannonball is still horizontal, meaning moving parallel to the earth’s
surface. And, since it’s above the
earth’s atmosphere, it won’t have lost any speed, so exactly the same thing
happens in the next second, and the next—it goes in a circular path. Newton had foreseen how a satellite would
move. 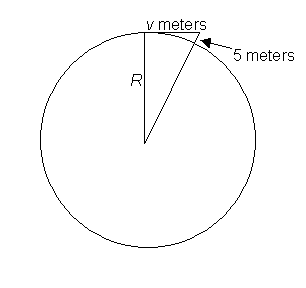
We can find how fast the cannonball must move to maintain the circular orbit by using Pythagoras’ theorem with the above diagram (which grossly exaggerates the speed so that you can see how to do the proof). Pythagoras gives:
(R + 5)2 = R2 + v2,
R2 + 10R + 25 = R2 + v2.
Newton knew (in different units) that R = 6400 km, so the 25 in the above equation can be neglected to give:
v2 = 10R = 10´6400´1000, so v = 8000.
The units are of course meters per second, on our diagram we show v as a distance, that traveled in the first second.
So the cannonball must move at 8 km. per second, or 5 miles per second to match the earth’s curvature—this is 18,000 mph, once round in a little less than an hour and a half. This is about right for a satellite in low earth orbit.
My applet illustrating the cannonball is here.
On to the Moon
It occurred to Newton one day (possibly because of a falling apple) that this familiar gravitational force we experience all the time here near the surface of the earth might extend outwards as far as the moon, and in fact might be the reason the moon is in a circular orbit. The radius of the moon’s orbit (384,000 km) and its speed in orbit (about 1 km per second) had long been known (see my notes here if you’re interested in how it was measured), so it was easy to find, using the same Pythagorean arguments as used for the cannonball above, that the moon “falls” 1.37 millimeters below a straight line trajectory in one second.
That is to say, the acceleration of the moon towards the center of the earth in its circular orbit is 1.37/5000, or about 1/3600, of the cannonball’s. But the radius of the moon’s orbit is about 60 times greater than the cannonball’s (which is just the radius of the earth, approximately). Since 60´60 = 3600, Newton concluded that the gravitational force decreased with distance as 1/r2.
The Universal Law of Gravitation
Newton then boldly extrapolated from the earth, the apple and the moon to everything, asserting that every body in the universe attracted every other body with a gravitational force that decreased with distance as 1/r2: a Universal Law of Gravitation.
But actually he knew more about the gravitational force: from the fact that bodies of different masses near the earth’s surface accelerate downwards at the same rate, using F = ma (his Second Law) if two bodies of different masses have the same acceleration they must be feeling forces in the same ratio as their masses (so a body twice as massive feels twice the gravitational force), that is, the gravitational force of attraction a body feels must be proportional to its mass. Now suppose we are considering the gravitational attraction between two bodies (as we always are), one of mass m1, one of mass m2. By Newton’s Third Law, the force body 1 feels from 2 is equal in magnitude (but of course opposite in direction) to that 2 feels from 1. If we think of m1 as the earth, the force m2 feels is proportional to m2, as argued above—so this must be true whatever m1 is. And, since the situation is perfectly symmetrical, the force must also be proportional to m1.
Putting all this together, the magnitude of the gravitational force between two bodies of masses m1 and m2 a distance r apart
F = Gm1m2/r2.
The constant G = 6.67´10-11 N.m2/kg2. It is important to realize that G cannot be measured by any astronomical observations. For example, g at the surface of the earth is given by
g = GmE/rE2
where mE is the mass and rE the radius of the earth. Notice that by measuring g, and knowing rE, we can find GmE. But this does not tell us what G is, since we don’t know mE! It turns out that this same problem arises with every astronomical observation. Timing the planets around the sun will give us GmSun. So we can figure out the ratio of the sun’s mass to the earth’s, but we can’t find an absolute value for either one.
The first measurement of G was made in 1798 by Cavendish, a century after Newton’s work. Cavendish measured the tiny attractive force between lead spheres of known mass. For details on how an experiment at the University of Virginia in 1969 improved on Cavendish’s work, click on the UVa Physics site here.
Cavendish said he was “weighing the earth” because once G is measured, he could immediately find mE from g = GmE/rE2, and then go on the find the mass of the sun, etc.
Kepler’s Laws
Actually, I exaggerated a little above in stating that Newton extrapolated from an apple, the earth and the moon to the universe. He also knew a few things about motion in the solar system that fitted in well with the inverse square law. For example, Kepler had found a law relating how long it took a planet to make one complete orbit around the sun (call it time T) to its distance from the sun (call it R). The relationship is
![]()
It is easy to show how this follows from the inverse square law if we assume the planets move in perfect circles, which they almost do. The acceleration of a planet moving at speed v in a circular orbit of radius R is v2/R towards the center. (This is easy to prove using the Pythagoras diagram above: just replace the 5 meters by ½ at2, the “horizontal” distance v by vt, write down Pythagoras’ theorem and take the limit of a very small time.)
Newton’s Second Law F = ma for a planet in orbit becomes:
![]()
Now the time for one orbit is T = 2pR/v, so dividing both sides of the equation above by R, we find:
![]()
This is Kepler’s Law.
In fact, Newton knew more than this—the planets’ orbits are more accurately describes as elliptic, and Newton had proved that a planetary orbit with an inverse square force is precisely an ellipse. (This neglects slight deviations caused by attraction towards other planets, and also a tiny relativistic effect explained by Einstein.)